How to solve Nonograms
Nonogram is a picture logic puzzle in which cells in a grid must be colored or left blank according to numbers at the side of the grid to reveal a hidden pixel art-like picture.
Here is an example of a Nonogram and how it looks when solved.
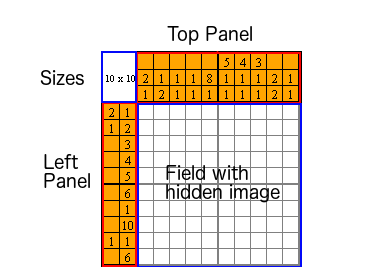
Firstly, let's get familiar with core elements. In the first image you can see two panels with numbers (left and top). If you compare it to the solved Nonogram, then it's clear that numbers from the left panel describe a number of painted cells in rows, meanwhile, numbers from the top panel correspond to cells in columns. For example, if there are numbers 2 and 1 (the first line), then there are 2 and 1 painted cells on the field that go in the same order.
How to understand which cells can be painted? Let's look at the left panel and find the biggest numbers. They are 6, 10, and 6. Then the following can be painted:
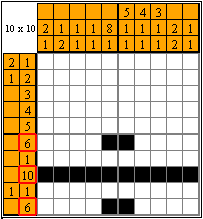
In this case, 10 without any doubt fills the whole line. With 6 it's slightly more difficult. If you try to imagine all the options where one could paint 6 cells, it appears that there are quite a few of them. So we can't be entirely sure which cells can be painted. But we could paint at least part of them! In order to do it, let's visualize the options from both ends:
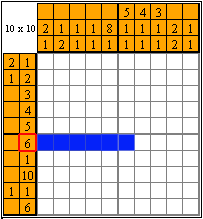
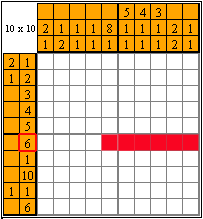
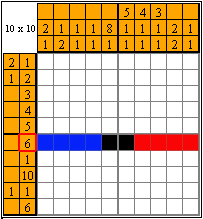
As you can see here, 2 cells appear at the intersection and there is no way we could paint 6 cells so these 2 cells would not be painted. Then there is no doubt that we can paint those cells.
In the same way, let's move further and check the top panel and paint the maximum number of cells which we can be entirely sure of.

Great, part of the image is already done. Let's cross out some of the cells now.
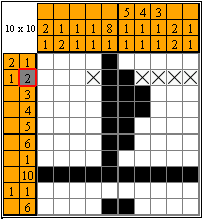
On the second line, it appears that number 2 is already painted, and since it's the last number in that line, then all the other cells till the end of the line can be crossed out, nothing else can be painted there. On the left, there is 1 cell that can be crossed out too, because number 1 can not be painted there as there needs to be at least one empty cell in between 1 and 2. Number 2 from the left panel needs to be crossed out too, we have already painted it.
Using the approach above, let's finish the remaining rows and columns.
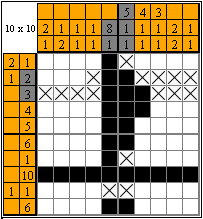
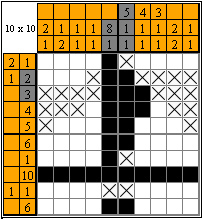
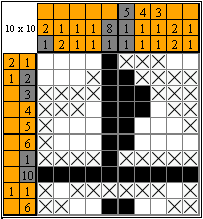
By painting or crossing out cells in which we are entirely sure, let's solve the Nonogram till the end.

Looks simple, but very entertaining at the same time.